Fan2Cube

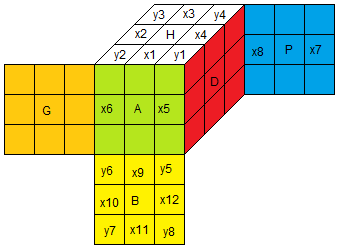
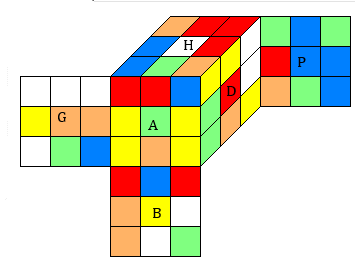
Maintenant vous savez bien résoudre le Rubik's Cube, Il faut passer à la vitesse supérieur. On explore la face cachée du Rubik's Cube (the dark side of the Cube comme the dark side of the Moon -Pink Floyd- !)
Quand on arrive au 3ième étage et quand on inverse (on oriente) les arêtes là il y a quelque chose qui devrait vous intriquer ...
Si vous remarquez bien, la formule utilisée inverse toujours deux arêtes !!! , et là on se pose plein de questions ....
- Existe-il des formules qui inversent une seule arête ?
Si la réponse est : oui => le problème est résolu (on inverse une par une, les arêtes)
Si la réponse est : non => cela poserait énormément de problèmes, car si on a une arête à orienter on ne peut pas alors orienter toutes les arêtes !!
Mais comme on arrive à restaurer le Cube avec des formules qui inversent 2 arêtes cela signifie que la situation inverser une seule arête n’est pas possible !!!
Mais alors peut-on la démontrer : Il est impossible d’inverser une seule arête ?
La réponse est « oui »
C’est une des lois du Rubik’s Cube :
*La loi des arêtes : Le nombre d’inversions (= le nombre d’orientations = le nombre de flips) des arêtes doit être pair.

Pour calculer le nombre d'orientations on se référence au diagramme ci-dessous :


-si la couleur dominante est sur le marquage 0, l'orientation vaut 0 (bien orienté)
-si la couleur dominante est sur le marquage 1, l'orientation vaut 1
-si la couleur dominante est sur le marquage -1, l'orientation vaut -1

Exemple :


(vr)=0, (bk)=1, (kr)=1, (jr)=1
(jv)=0, (jo)=0, (jk)=1, (br)=1
(ko)=0, (vo)=1, (bv)=0, (bo)=0
le nonbre d'orientations des arêtes est 6 (c'est un nombre pair)