et pourtant ce sont des choses très différentes.
Voyons voir :
Voici un état (une sorte de motif) s du Rubik's Cube.
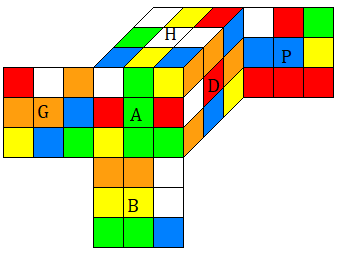
qui est codé mathématiquement s=(u,x,v,y) où
u=permutation des arêtes (des pièces)
x=orientation des arêtes (vecteur)
v=permutation des sommets (des pièces)
x=orientation des sommets (vecteur)
Et G l'ensemble de ces états munis la loi de composition '.' :
(u,x,v,y)(u',x',v',y') = (uu', x+u(x'), vv', y+v(y'))
forme un groupe (G,.) le groupe d'états (c'est le groupe du Rubik's Cube par définition) .
De l'autre côté, soit X = {1,2,3,...,48} l'ensemble des 48 autocollants (stickers) numérotés ainsi.
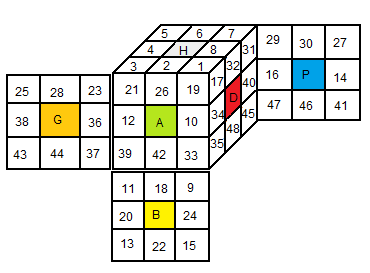
à chaque rotation de base {H,B,A,P,G,D} on associe une permutation (des autocollants) :
pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(9,37,3,17)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
On a donc 6 permutations de SX.
Soit Λ l'ensemble des permutations engendrées par les 6 permutations {PH, PB, PA, PP,PG, PD}
Λ = < PH, PB, PA, PP,PG, PD >
(Λ,.) le groupe de permutations
p.q = pq = qop
Il se trouve que G et Λ ont le même nombre éléments ==> d'où la confusion permutations = états !!!
PH c'est une application de Sx dans SX il n'y a rien à voir avec le truc (u,x,v,y) !!!!
Attention !! ne pas confondre non plus les permutation u,v des pièces avec les permutations des autocollants PH , PB ,
...
Souvent on confond aussi A avec pA !! et pourtant A est une rotation un élément de M (l'ensemble des formules)
pA est une permutation un truc de Sx
et M = < H,B,A,P,G,D > où {H,B,A,P,G,D} rotations de base
(M,.) le groupe de formules
V.T = VT ; concaténation
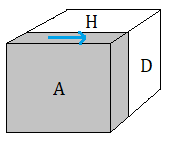
Voici les 3 images qui représentent les 3 concepts :
(a) rotation (formule) :
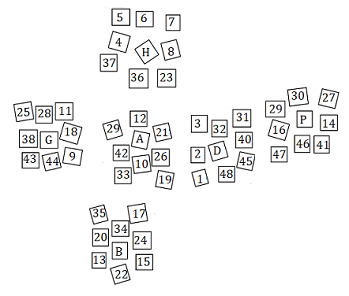
(b) permutation :
(c) état :
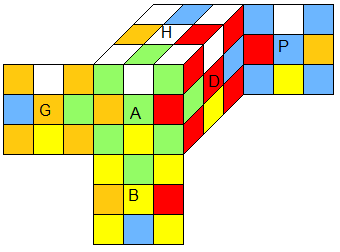
1) dans (a) on ne voit pas les sommets ni des arêtes mais seulement les faces H,A, ....
2) dans (b) on ne voit pas non plus les sommets ni les arêtes, ni les couleurs, mais seulement des autocollants numérotés éparpillés sur la table.
3) dans (c) on voit les sommets, les arêtes, et leurs orientations ...
Ces trois images (a),(b),(c) sont très différentes donc il n'y a aucune raison de confondre : les rotation avec les permutations et les états !!



