Confusion entre état et classe (orbite)
Publié : Mar 4/05/2021 11:17
Le Pocket et le nombre 3674160
====================================
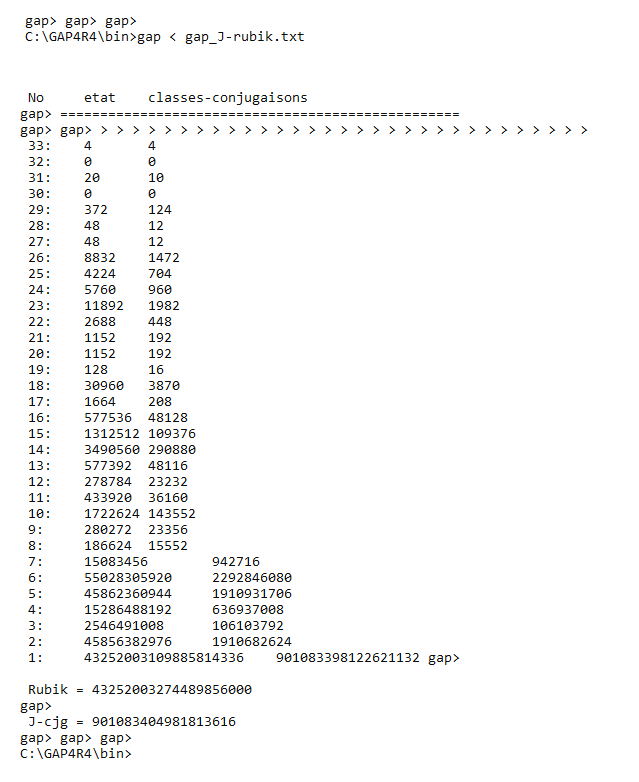
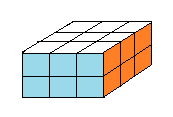
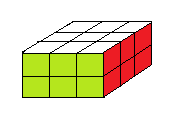
Si vous cherchez le nombre d'états du Pocket sur internet vous verrez peut-être le nombre 3674160 au lieu de 88179840.
Observons les trois images (a), (b) et (c) ci-dessous
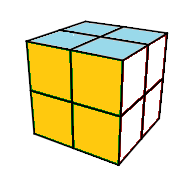
image (a)
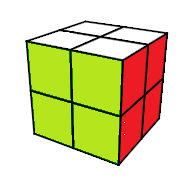
image (b)
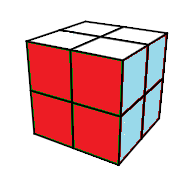
image (c)
Pour un Jury de compétition ces états représentent l'état résolu.
Et le nombre d'états (dans le sens des Jurys ) est m=3674160
En réalité m=3674160 est le nombres de classes d'équivalence !
Pour comprendre il faut revenir tout au début de l'histoire ....
En 1993, Jerry BRYAN écrivait un article expliquant le calcul du diamètre du Pocket (cet article est mal compris par beaucoup de gens).
Pour ce faire BRYAN a classé les états du Pocket suivant le critère nommé D-symétrie, plus précisément suivant le groupe de déplacement D du cube (qui contient 24 éléments).
D agit librement (= seul id a des points fixes) sur G
G x D -> G
(s,f) -> s•f = t
à '•' on associe la relation d'équivalence ~ suivante:
deux états s , t sont dans la même classe ssi:
s ~ t ⇔ ∃f∈D tel que s•f = t
La formule de Burnside donne:
w = 1/|D| ∑|Ff| ; somme sur f∈ D
comme l'action est libre Ff = Ø si f ≠ id et Fid = G
w = |G|/24 = 88179840/24 = 3674160
du coup les états du Pocket sont partagés en 3674160 D-classes (de 24 éléments chaque une)
Ces classes forme un graphe T dont le diamètre est le même que celui du Pocket :
BRYAN a fait un programme informatique et a trouvé le diamètre de T qui valait 14 donc le diamètre du Pocket aussi,
Les distances du graphe T:
Distance D-classes
==============================
0 ==> 1
1 ==> 6
2 ==> 27
3 ==> 120
4 ==> 534
5 ==> 2256
6 ==> 8969
7 ==> 33058
8 ==> 114149
9 ==> 360508
10 ==> 930588
11 ==> 1350852
12 ==> 782536
13 ==> 90280
14 ==> 276
===========================
Total D-classes : 3674160
Comme le diamètre du Pocket c'est le diamètre du graphe d'états ===> d'où la confusions 3674160 est le nombre d'états du Pocket.
D'autre part, dans une compétition, le Jury considère qu'un élément s ∈ cl(e) de la classe de e est l'état résolu d'où la confusion entre classe et état
On a fait aussi un programme qui calcule directement le diamètre du Pocket et ça donne
Les distances du graphe du Pocket :
distance ==> nombre d'états
=================================
0 ==> 1
1 ==> 12
2 ==> 114
3 ==> 924
4 ==> 6539
5 ==> 39528
6 ==> 199926
7 ==> 806136
8 ==> 2761740
9 ==> 8656152
10 ==> 22334112
11 ==> 32420448
12 ==> 18780864
13 ==> 2166720
14 ==> 6624
===============================
total états: 88179840
Voici un script en GAP qui calcule le nombre d'états du Pocket


 (confusion entre état et classe)
(confusion entre état et classe)
====================================
Si vous cherchez le nombre d'états du Pocket sur internet vous verrez peut-être le nombre 3674160 au lieu de 88179840.
Observons les trois images (a), (b) et (c) ci-dessous

image (a)

image (b)

image (c)
Pour un Jury de compétition ces états représentent l'état résolu.
Et le nombre d'états (dans le sens des Jurys ) est m=3674160
En réalité m=3674160 est le nombres de classes d'équivalence !
Pour comprendre il faut revenir tout au début de l'histoire ....
En 1993, Jerry BRYAN écrivait un article expliquant le calcul du diamètre du Pocket (cet article est mal compris par beaucoup de gens).
Pour ce faire BRYAN a classé les états du Pocket suivant le critère nommé D-symétrie, plus précisément suivant le groupe de déplacement D du cube (qui contient 24 éléments).
D agit librement (= seul id a des points fixes) sur G
G x D -> G
(s,f) -> s•f = t
à '•' on associe la relation d'équivalence ~ suivante:
deux états s , t sont dans la même classe ssi:
s ~ t ⇔ ∃f∈D tel que s•f = t
La formule de Burnside donne:
w = 1/|D| ∑|Ff| ; somme sur f∈ D
comme l'action est libre Ff = Ø si f ≠ id et Fid = G
w = |G|/24 = 88179840/24 = 3674160
du coup les états du Pocket sont partagés en 3674160 D-classes (de 24 éléments chaque une)
Ces classes forme un graphe T dont le diamètre est le même que celui du Pocket :
BRYAN a fait un programme informatique et a trouvé le diamètre de T qui valait 14 donc le diamètre du Pocket aussi,
Les distances du graphe T:
Distance D-classes
==============================
0 ==> 1
1 ==> 6
2 ==> 27
3 ==> 120
4 ==> 534
5 ==> 2256
6 ==> 8969
7 ==> 33058
8 ==> 114149
9 ==> 360508
10 ==> 930588
11 ==> 1350852
12 ==> 782536
13 ==> 90280
14 ==> 276
===========================
Total D-classes : 3674160
Comme le diamètre du Pocket c'est le diamètre du graphe d'états ===> d'où la confusions 3674160 est le nombre d'états du Pocket.
D'autre part, dans une compétition, le Jury considère qu'un élément s ∈ cl(e) de la classe de e est l'état résolu d'où la confusion entre classe et état
On a fait aussi un programme qui calcule directement le diamètre du Pocket et ça donne
Les distances du graphe du Pocket :
distance ==> nombre d'états
=================================
0 ==> 1
1 ==> 12
2 ==> 114
3 ==> 924
4 ==> 6539
5 ==> 39528
6 ==> 199926
7 ==> 806136
8 ==> 2761740
9 ==> 8656152
10 ==> 22334112
11 ==> 32420448
12 ==> 18780864
13 ==> 2166720
14 ==> 6624
===============================
total états: 88179840
Voici un script en GAP qui calcule le nombre d'états du Pocket
Code : Tout sélectionner
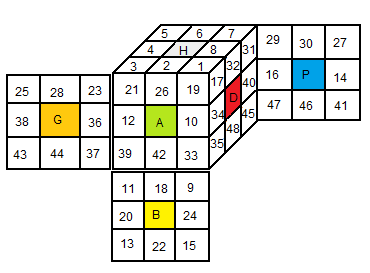
#gap_pocket.txt
# 5 7
# H
# 3 1
#25 23|21 19|17 31|29 27
# G | A | D | P
#43 37|39 33|35 45|47 41
# 11 9
# B
# 13 15
# Pocket=le groupe Pocket (= Rubik sans arêtes)
pH := (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (1,29,15,33)(17,31,45,35)(19,7,47,9);
pPsi := (1,17,19);
LAMBDAPLUS := Group( pH, pB, pA, pP, pG, pD, pPsi );
LAMBDA := Group( pH, pB, pA, pP, pG, pD );
N := 3 ;;
Print( "\n" );
Print( "|LAMBDA+| = ",Size( LAMBDAPLUS ), "\n" );
Print( "|LAMBDA| = ", Size( LAMBDA ) , "\n" );
Print( "N = ", N , "\n" );
Print( "|G+| = ", Factorial(8) * (3^8) , "\n" );
Print( "|G| = |G+|/N = ",( Factorial(8) * (3^8) ) / N , "\n" );
 (confusion entre état et classe)
(confusion entre état et classe)