LA PARITE :
¤ La parité (le problème de parité) : c'est un état µ où l'on viole la loi de parité, cet état µ est obtenu par
une formule contenant au moins une rotation non-standard (non-base).
exemple
Helicopter:
* Rotations de base (rotations stardards) : 12 arêtes à 180°
* Loi de parité : sig(sommets) = sig(feuilles)
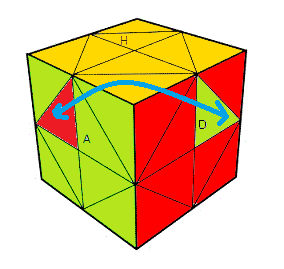
DG .(doAo'd'A) .GD (contient les rotations non-base : o, d, ... à 60°)
Square-1:
* Rotations de base (rotations standards) : {3, 3B, S, Q, E, T}
Avec :
S = 1/3/-1 , Q = 1/3B/-1
E = -B/3/B , T = -B/3B/B
* Loi de parité : sig(sommets) = sig(arêtes)
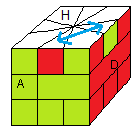
(HA)<->(HD) = /-3/3B/-3B/3B/2/2B/-2/4/-2B/2B/-1+4B/6-3B/6/6+3B
(contient les rotations non-base : -2/, 4/, -1+4B/ ....)
LA SINGULARITE :
¤ La singularité (l'état légal renommé) : c'est un état légal µ où l'on ne viole aucune loi, cet état µ est obtenu par
une formule ne contenant que les rotations de base (rotations standards). Cet état µ particulier est simplement renommé "singulier"
exemple
Void Cube:
* Rotations de base (rotations standards) : {H,h,a,P,G,D}
* Pas de loi de parité !!
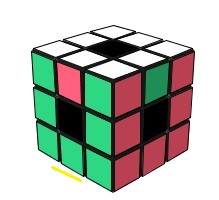
(HA)<->(HD) = (aH)²(aH')²aH²(aH')² (arêtes)
Revenge:
* Rotations de base (rotations standards) : {H,B,A,P,G,D,h,b,a,p,g,d}
* Loi de parité : sig(sommets) = sig(centres)
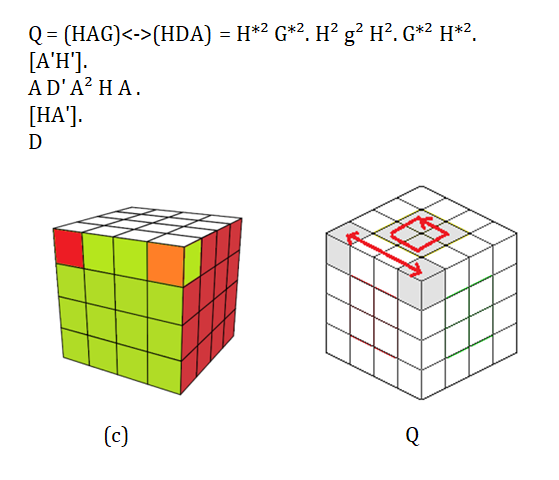
REMARQUE : il y a très peu de twists qui génèrent les parités (le problème de parité) , il n'y a que 3
-> le Square-1
-> le Helicopter (et sa famille)
-> le SuperFloppy Cube



