Construction le groupe du Rubik's Cube G
Publié : Mar 30/04/2024 12:19
Construction le groupe du Rubik's Cube G
On oriente le Cube ainsi:
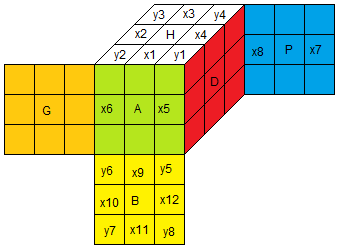
Haut=blanc, Bas=jaune, Avant=vert, Postérieur=klein, Gauche=orange, Droite=rouge.
On pose:
a) G+ = S12 x Z212 x S8 x Z38
où
Sn = les permutations à n objets (Sn , .) où la loi '.' est : p.q = pq = q o p
Zk = le groupe modulo k (Z/kZ,+)
s=(u,x,v,y) €G+, u€S12, x€Z212, v€S8, y€Z38
x = (x1, x2, ... , x12)
y = (y1, y2, ... , y8)
xi = 0,1 si la couleur dominante est sur 0,1
yi = 0,1,-1 si la couleur dominante est sur 0,1,-1
s.s' = ss' = (u,x,v,y)(u',x',v',y') = (uu',x+u(x'),vv',y+v(y'))
où
uu' = u'ou
u(x) = (xu(1), xu(2), ...) ; permutatuion des xi par u
Les éléments de G+ se nomment configuration
(G+,.) le groupe des configurations du Rubik's Cube
b) M = <H,B,A,P,G,D>
où H,B,A,P,G,D les rotations de base
Les éléments de M se nomment formule
Une formule V est donc une suite finie de rotations de base respectant la règle :
HH', H'H, BB', B'B, AA',A'A, PP', P'P, GG', G'G, DD', D'D sont interdits dans une formule
On pose : HH' = H'H = BB' = B'B = AA' = A'A = PP' = P'P = GG' = G'G = DD' = D'D = I
exemple:
HDH'D'APG² ; OK
DHH'PAG ; interdit car HH'
Dans M on munit la loi concaténation '.'
1) V,T ==> VT€M loi interne
2) IV = VI = V ; I=élément neutre
3) V = HDH'D'APG² ==> V' = G'²P'A'DHD'H' inverse de V
VV' = V'V = I
4) V,T,S , (VT)S = V(TS) ; associativité
(M,.) un groupe
(M,.) le groupe des formules du Rubik's Cube
c) On définit une action '•' de M dans G+ ainsi
G+ x M --> G+
(s,V) --> s•V = t
Vérifiant les 4 axiomes suivants:
A1: s•I = s ; élément neutre
A2: (s•V)•T = s•(VT) ; associativité
A3: a donné, fixé
a•V=a ==> V=I ; librement
A4: s•(VT) = (s•V)(s•T) ; compatibilité
d) Par définition : le groupe du Rubik's Cube G est :
G = {s€G+ | s=e•V , V€M} ; e=configuration résolu
Les éléments de G se nomment état
G = ce sont des configurations provenant de M (à partir de e) .
e) s=(u,x,v,y) €G+, On pose :
(F) x=0 (mod 2)
(T) y=0 (mod 3)
(P) sig(u) = sig(v)
Théorème fondamental de la Cubologie :
G = {s€G+| s vérifie (F), (T), (P)}
G = ce sont des configurations vérifiant les trois lois (F), (T), (P).
On oriente le Cube ainsi:
Haut=blanc, Bas=jaune, Avant=vert, Postérieur=klein, Gauche=orange, Droite=rouge.
On pose:
a) G+ = S12 x Z212 x S8 x Z38
où
Sn = les permutations à n objets (Sn , .) où la loi '.' est : p.q = pq = q o p
Zk = le groupe modulo k (Z/kZ,+)
s=(u,x,v,y) €G+, u€S12, x€Z212, v€S8, y€Z38
x = (x1, x2, ... , x12)
y = (y1, y2, ... , y8)
xi = 0,1 si la couleur dominante est sur 0,1
yi = 0,1,-1 si la couleur dominante est sur 0,1,-1
s.s' = ss' = (u,x,v,y)(u',x',v',y') = (uu',x+u(x'),vv',y+v(y'))
où
uu' = u'ou
u(x) = (xu(1), xu(2), ...) ; permutatuion des xi par u
Les éléments de G+ se nomment configuration
(G+,.) le groupe des configurations du Rubik's Cube
b) M = <H,B,A,P,G,D>
où H,B,A,P,G,D les rotations de base
Les éléments de M se nomment formule
Une formule V est donc une suite finie de rotations de base respectant la règle :
HH', H'H, BB', B'B, AA',A'A, PP', P'P, GG', G'G, DD', D'D sont interdits dans une formule
On pose : HH' = H'H = BB' = B'B = AA' = A'A = PP' = P'P = GG' = G'G = DD' = D'D = I
exemple:
HDH'D'APG² ; OK
DHH'PAG ; interdit car HH'
Dans M on munit la loi concaténation '.'
1) V,T ==> VT€M loi interne
2) IV = VI = V ; I=élément neutre
3) V = HDH'D'APG² ==> V' = G'²P'A'DHD'H' inverse de V
VV' = V'V = I
4) V,T,S , (VT)S = V(TS) ; associativité
(M,.) un groupe
(M,.) le groupe des formules du Rubik's Cube
c) On définit une action '•' de M dans G+ ainsi
G+ x M --> G+
(s,V) --> s•V = t
Vérifiant les 4 axiomes suivants:
A1: s•I = s ; élément neutre
A2: (s•V)•T = s•(VT) ; associativité
A3: a donné, fixé
a•V=a ==> V=I ; librement
A4: s•(VT) = (s•V)(s•T) ; compatibilité
d) Par définition : le groupe du Rubik's Cube G est :
G = {s€G+ | s=e•V , V€M} ; e=configuration résolu
Les éléments de G se nomment état
G = ce sont des configurations provenant de M (à partir de e) .
e) s=(u,x,v,y) €G+, On pose :
(F) x=0 (mod 2)
(T) y=0 (mod 3)
(P) sig(u) = sig(v)
Théorème fondamental de la Cubologie :
G = {s€G+| s vérifie (F), (T), (P)}
G = ce sont des configurations vérifiant les trois lois (F), (T), (P).