Fan2Cube

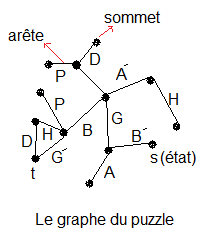
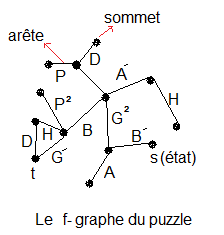
¤ Une configuration des autocollants est une sort de motif.

¤ Un état = une configuration provenant des rotations de base en respectant l'orientation du Cube et visuellement distingue.

¤ Position , Permutation , ... ==> état = motif = configuration (des autocollantes)

¤ Mouvement ==> rotation

¤ Mouvement = mélange = manoeuvre = formule = une suite finie de rotations de base (et leur inverse sous-entendu)

¤ Coin ==> Sommet

¤ Algorithme ==> Formule , mais on dit l'algorithme de la résolution.

¤ Algorithme de résolution = Une suite finie d'actions (comme une recette de la cuisine)

¤ Action = placer, pivoter, déplacer, ranger, permuter, orienter, glisser, ....

¤ Pivoter un sommet (twist), renverser une arête (flip) , retourner une arête (flip)

¤ Ranger = bien placer, bien orienter

¤ Glisser = déplacer sans changer les orientations

¤ Rotations de base (= rotations standards) {H,B,A,P,G,D}

¤ Formule = Une suite finie de rotations de base et leur inverse, exemple
T = DHD'H' APGB
Q = H²D'G²PA'

donc
V = HdBP'a'G,
S = PG tH GA
ne sont pas vraiment des formules proprement parler !!!, puisqu' elles contiennent des rotations non-standards. Mais par abuse
de langage on dit quand même des formules.


¤ Longueur d'une formule Q = le nombre de rotations qu' elle compose, on note |Q| longueur de Q
ex:
|A|=1, |A²|=2, |I|=0 (car il n'y a aucune rotation dans I)
Q = H²D'G²PA' , |Q|= 7

¤ état-parité ==> l'état où on viole la loi de parité comme dans l' Héllicopter, Square-1, Super Floppy ....
¤ état-singulier ==> l'état légale particulier renommé .

¤ Graphe du twist (le graphe de Cayley) :


==> Les sommets du graphe sont des états du twists.
==> Les arêtes du graphe sont des rotations de base ou leur inverse {H,B,A,P,G,D,H',B',A',P',G',D'}
autrement dit une arête (s,t) du graphe est reliée par une rotation de base ou son inverse : s•X=t ou s•X'=t, X rotation de base



¤ chemin(s,t) = une suite finie de rotations qui lie s à t
exemple
chemin1(s,t) = PA'GHB'G²
chemin2(s,t) = HP'BD

¤ Distance (s,t) = plus court chemin entre s et t
exemple
Distance(s,t) = 4

¤ Diamètre = la plus grande distance du graphe


Diamètre = 3


¤ f-Graphe du twist (le graphe de Cayley en f-rotation) :


==> Les sommets du graphe sont des états du twists.
==> Les arêtes du graphe sont des rotations de base ou leur inverse ou leur carré {H,B,A,P,G,D,H',B',A',P',G',D' , H²,B²,A²,P²,G²,D²}
autrement dit une arête (s,t) du graphe est reliée par une rotation de base ou son inverse on son carré : s•X=t ou s•X'=t ou s•X²=t , X rotation de base