Une formule et l'écriture d'une formule.
Publié : Mar 9/06/2020 11:46
Vous êtes peut-être très intrigué de savoir la différence entre "formule" et "écriture" d'une formule !
Pourquoi introduit-on le mot "écriture" , pourquoi ne pas utiliser seulement le mot "formule" ?
et quelle est la différence entre "formule" et "écriture" d'une formule ?
On sait que le nombre d'états du Rubik's Cube est fini et vaut: 43 252 003 274 489 856 000
On sait qu'une formule engendre un état.
On aimerait bien que l'ensemble des formules soit fini et aie le même nombre d'élements que le nombre d'états du Rubik's Cube.
Donc si on concidère que deux formules sont différentes quand elles engendrent un même état, alors
l'ensemble des formules sera infini !! (A' ≠ A3 ≠ A7 ≠ A11 ....)
Comme l'ensemble des états est fini, pour rendre l'ensemble des formules fini on utilise la technique suivante:
1) Soit s un état, on met toutes les formules qui engendrent s dans une boite, on aura ainsi un nombre fini de boites
puisqu'on a un nombre fini d'états,
2) On selecte alors une formule de la boite par exemple N et on la met dans un coffre à la banque, puis on déclare les autres formules dans la boite sont des écritures de N.
Donc la formule N gènère l'état s et s provient de N.
Observons le dessin ci-dessous
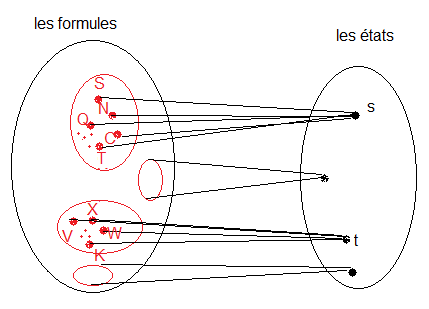
Plusieurs formules donnent le même état s.
Q,N,S,C,T , ... ===> s
On regroupe les formules qui donnent l'état s dans une boite {Q,N,S,C,T,....}
On en sélecte une par ex N et on la met N dans un coffre à la banque , puis les autres on déclare ce sont des écritures de N
autrement dit Q,S,C,T ... sont des écriture de N : Q=S=C=T= ....
De même plusieurs formules donnent le même état t
V,X,K,W, ... ===> t
On regroupe les formules qui donnent l'état t dans une boite {V,X,K,W ....}
On en sélecte une par exemple K et on la met K dans un coffre à la banque , puis les autres on déclare ce sont des écritures de K
autrement dit V,X,W ... sont des écriture de K : V=X=W= ...
On fait de même pour les autres états
ainsi on trouve
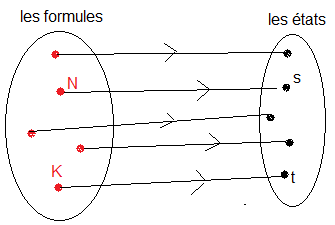
N gènère l'état s et s provient de N et on note: s = e•N
K gènère l'état t et t provient de K et on note: t = e•K
Ainsi chaque formule gènère un état et chaqu'état provient d'une formule.
On s'est déjà rencontré ce genre de situation :
- l'inverse de 2 : un seul l'inverse de 2, mais il a plusieurs d'écritures: 1/2 = 0,5 = 2/4 = 3/6 = ...
- le vecteur nul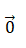
: un seul vecteur nul, mais il a plusieurs d'écritures: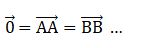
- permutation identique id : une seule permutation identique, mais elle a plusieurs d'écritures: id = (a) = (b) = ....
Mais on ne manipule que les écritures (Q,S,C,T,...) , (V,X,W,...) puisque les formules N,K, ... sont dans un coffer à la banque qu'on ne touche pas ...
Du coup le concept "formule" est abstraire puisqu'on ne touche jamais une formule, on sait seulement à chaqu'état on a une formule (qui se trouve dans un coffre à la banque) et à chaque formule on a un état.
Pour avoir un état on utilise les écritures ....
Finalement par abuse de langage on dit écriture pour formules.
Résumons :
1) Chaqu' état provient d'une seule formule
2) Chaque formule engendre un seul état.
3) Le nombre de formules est égale au nombre d'états
4) Pour chaque formule, il y a plusieurs d'écritutres, parmi ces écritures il y a des plus courtes (longueur minimale)
5) En pratique et par abuse de language on dit:
==> "il y a plusieurs formules qui donnent le même état"
au lieu de
==> "il a y plusieurs écritures pour une formule".
Pourquoi introduit-on le mot "écriture" , pourquoi ne pas utiliser seulement le mot "formule" ?
et quelle est la différence entre "formule" et "écriture" d'une formule ?
On sait que le nombre d'états du Rubik's Cube est fini et vaut: 43 252 003 274 489 856 000
On sait qu'une formule engendre un état.
On aimerait bien que l'ensemble des formules soit fini et aie le même nombre d'élements que le nombre d'états du Rubik's Cube.
Donc si on concidère que deux formules sont différentes quand elles engendrent un même état, alors
l'ensemble des formules sera infini !! (A' ≠ A3 ≠ A7 ≠ A11 ....)
Comme l'ensemble des états est fini, pour rendre l'ensemble des formules fini on utilise la technique suivante:
1) Soit s un état, on met toutes les formules qui engendrent s dans une boite, on aura ainsi un nombre fini de boites
puisqu'on a un nombre fini d'états,
2) On selecte alors une formule de la boite par exemple N et on la met dans un coffre à la banque, puis on déclare les autres formules dans la boite sont des écritures de N.
Donc la formule N gènère l'état s et s provient de N.
Observons le dessin ci-dessous
Plusieurs formules donnent le même état s.
Q,N,S,C,T , ... ===> s
On regroupe les formules qui donnent l'état s dans une boite {Q,N,S,C,T,....}
On en sélecte une par ex N et on la met N dans un coffre à la banque , puis les autres on déclare ce sont des écritures de N
autrement dit Q,S,C,T ... sont des écriture de N : Q=S=C=T= ....
De même plusieurs formules donnent le même état t
V,X,K,W, ... ===> t
On regroupe les formules qui donnent l'état t dans une boite {V,X,K,W ....}
On en sélecte une par exemple K et on la met K dans un coffre à la banque , puis les autres on déclare ce sont des écritures de K
autrement dit V,X,W ... sont des écriture de K : V=X=W= ...
On fait de même pour les autres états
ainsi on trouve
N gènère l'état s et s provient de N et on note: s = e•N
K gènère l'état t et t provient de K et on note: t = e•K
Ainsi chaque formule gènère un état et chaqu'état provient d'une formule.
On s'est déjà rencontré ce genre de situation :
- l'inverse de 2 : un seul l'inverse de 2, mais il a plusieurs d'écritures: 1/2 = 0,5 = 2/4 = 3/6 = ...
- le vecteur nul
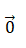: un seul vecteur nul, mais il a plusieurs d'écritures: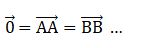- permutation identique id : une seule permutation identique, mais elle a plusieurs d'écritures: id = (a) = (b) = ....
Mais on ne manipule que les écritures (Q,S,C,T,...) , (V,X,W,...) puisque les formules N,K, ... sont dans un coffer à la banque qu'on ne touche pas ...
Du coup le concept "formule" est abstraire puisqu'on ne touche jamais une formule, on sait seulement à chaqu'état on a une formule (qui se trouve dans un coffre à la banque) et à chaque formule on a un état.
Pour avoir un état on utilise les écritures ....
Finalement par abuse de langage on dit écriture pour formules.
Résumons :
1) Chaqu' état provient d'une seule formule
2) Chaque formule engendre un seul état.
3) Le nombre de formules est égale au nombre d'états
4) Pour chaque formule, il y a plusieurs d'écritutres, parmi ces écritures il y a des plus courtes (longueur minimale)
5) En pratique et par abuse de language on dit:
==> "il y a plusieurs formules qui donnent le même état"
au lieu de
==> "il a y plusieurs écritures pour une formule".