La formule J = A[DH]A'H
Publié : Lun 24/02/2020 16:49
La formule J = A[DH]A'H
Avant de comprendre les propriétés de J, on va rappeler ce que c'est l'algorithme minimal :
Par définition l'algorithme minimal est:
1. Placer les arêtes : V
2. Placer les sommets : V
3. Pivoter les arêtes: V²
4. Pivoter les sommets : V4
où V est une formule.
La formule V qui se trouve dans l'algorithme minimal se nomme formule "première"
J est une formule première et de plus elle est minimale ! (sa longueur est plus courte)
Donc à elle seule on peut (ou un Robot) restaurer le Cube .
J = A[DH]A'H
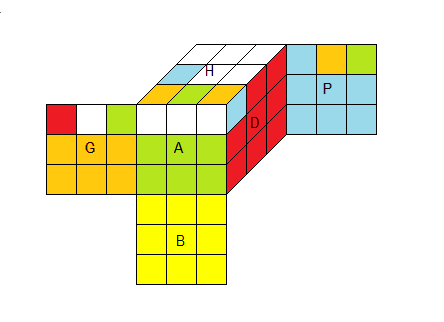
Quelques notations:
1) x, y, z, ... minuscules désignent les arêtes, X, Y, Z, ... majuscules désignent les sommets
2) (x,y)=permuter deux arêtes x,y, (X,Y)=permuter deux sommets X,Y
3) x+ pivoter l'arête x, X+ pivoter le sommet X dans le sens horaire
En regardant l'état (les stickers) de θ, on voit que la formule θ est de la forme
J = (x+, y) z+ (X, Y-) Z+
==> On va regarder ce qui se passe pour les arêtes sans s'occuper de leurs orientations.
J permute 2 arêtes donc on peut placer toutes les arêtes par J (avec les conjugaisons bien sûr)
==> On va regarder ce qui se passe pour les sommets sans s'occuper de leurs orientations.
J permute 2 sommets mais dérange aussi les arêtes, il faut utiliser J en un nombre pair de fois pour ne pas déranger les arêtes. C'est ici que la loi de parité du Rubik's Cube intervient :
Loi de parité : Si les arêtes sont bien placées (pas forcement bien orientées) alors pour placer les sommets on utilise un nombre pair de permutation (X,Y).
Donc quand les arêtes sont bien placées , on est sûr d'utiliser un nombre pair de fois J, donc les arêtes ne sont pas dérangées.
==> On va regarder l'orientation des les arêtes.
J² pivote 2 arêtes en effet , soient trois arêtes x,y, z et '==>' signifie on applique J
x,y, z ==> y+, x, z+ ==> x+, y+, z
on a bien pivoté 2 arêtes donc on peut pivoter toutes les arêtes par J² . C'est ici qu'intervient la loi des flips
Loi des flips : Le nombre de flips est pair
Donc avec J² on pivote les 12 arêtes
==> On va regarder l'orientation des les sommets.
J4, pivote 3 sommets en effet , soient trois sommets X,Y, Z et '==>' signifie on applique J
X,Y, Z ==> Y, X-, Z+ ==> X-, Y-, Z++
==> Y-, X--, Z+++ ==> X--, Y--, Z++++
= X+, Y+, Z+
on a bien pivoté 3 sommets donc on peut pivoter toutes les sommets par J4 . C'est ici qu'intervient la loi des twists
Loi des twists : Le nombre de twists est un multiple de 3, autrement dit
Soit on pivote 2 sommets dans le sens contraire
Soit on pivote 3 sommets dans le même sens
Donc avec J4 on pivote tous les sommets
NOTE: J4 ne touche pas les arêtes, ne déplace pas les sommets, il pivote seulement les sommets.
Avant de comprendre les propriétés de J, on va rappeler ce que c'est l'algorithme minimal :
Par définition l'algorithme minimal est:
1. Placer les arêtes : V
2. Placer les sommets : V
3. Pivoter les arêtes: V²
4. Pivoter les sommets : V4
où V est une formule.
La formule V qui se trouve dans l'algorithme minimal se nomme formule "première"
J est une formule première et de plus elle est minimale ! (sa longueur est plus courte)
Donc à elle seule on peut (ou un Robot) restaurer le Cube .
J = A[DH]A'H

Quelques notations:
1) x, y, z, ... minuscules désignent les arêtes, X, Y, Z, ... majuscules désignent les sommets
2) (x,y)=permuter deux arêtes x,y, (X,Y)=permuter deux sommets X,Y
3) x+ pivoter l'arête x, X+ pivoter le sommet X dans le sens horaire
En regardant l'état (les stickers) de θ, on voit que la formule θ est de la forme
J = (x+, y) z+ (X, Y-) Z+
==> On va regarder ce qui se passe pour les arêtes sans s'occuper de leurs orientations.
J permute 2 arêtes donc on peut placer toutes les arêtes par J (avec les conjugaisons bien sûr)
==> On va regarder ce qui se passe pour les sommets sans s'occuper de leurs orientations.
J permute 2 sommets mais dérange aussi les arêtes, il faut utiliser J en un nombre pair de fois pour ne pas déranger les arêtes. C'est ici que la loi de parité du Rubik's Cube intervient :
Loi de parité : Si les arêtes sont bien placées (pas forcement bien orientées) alors pour placer les sommets on utilise un nombre pair de permutation (X,Y).
Donc quand les arêtes sont bien placées , on est sûr d'utiliser un nombre pair de fois J, donc les arêtes ne sont pas dérangées.
==> On va regarder l'orientation des les arêtes.
J² pivote 2 arêtes en effet , soient trois arêtes x,y, z et '==>' signifie on applique J
x,y, z ==> y+, x, z+ ==> x+, y+, z
on a bien pivoté 2 arêtes donc on peut pivoter toutes les arêtes par J² . C'est ici qu'intervient la loi des flips
Loi des flips : Le nombre de flips est pair
Donc avec J² on pivote les 12 arêtes
==> On va regarder l'orientation des les sommets.
J4, pivote 3 sommets en effet , soient trois sommets X,Y, Z et '==>' signifie on applique J
X,Y, Z ==> Y, X-, Z+ ==> X-, Y-, Z++
==> Y-, X--, Z+++ ==> X--, Y--, Z++++
= X+, Y+, Z+
on a bien pivoté 3 sommets donc on peut pivoter toutes les sommets par J4 . C'est ici qu'intervient la loi des twists
Loi des twists : Le nombre de twists est un multiple de 3, autrement dit
Soit on pivote 2 sommets dans le sens contraire
Soit on pivote 3 sommets dans le même sens
Donc avec J4 on pivote tous les sommets
NOTE: J4 ne touche pas les arêtes, ne déplace pas les sommets, il pivote seulement les sommets.