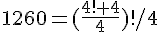Pour chaque formule on peut associer une longueur, la façon la plus naturelle c'est compter le nombre de rotations que compose
la formule, par exemple
V = HAB²P'G² , longueur(V)=7 on note aussi |V|=7 on dit qu'on a utilisé la métrique quart, 7 q-rotations
Il y a aussi une autre manière de compter les rotations , on compte A² pour 1 c'est-à-dire |A²|=1 donc dans ce cas
|V|= 5f on dit qu'on a utilisé la métrique "face" , 5 f-rotations. Bref ce n'est pas important les vocabulaires "métrique-quart", "métrique-face"
Pour nous on va prendre la métrique quart, la plus naturelle |V|=7 (q-rotations)
Remarque: il se peut qu'on a deux formules identiques mais qui ont de longueur différente !! par ex: A3 = A' et
|A3|=3 et |A'|=1
Une question naturelle est: une formule donnée, trouver une formule une plus courte, minimale ? (*=minimale)
Formules célèbres
1. Le SuperFlip Φ : toutes les arêtes sont renversées.
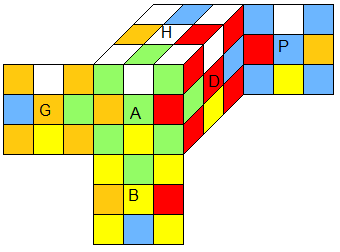
Φ = D'H²PG' AH'PBA HB'GB² A'DP'BA' H'P'HB' (trouvé par Michael Reid par ordinateur), en 1995 Jerry Bryan démontre que c'est une formule minimale
|Φ|=24
Le SupeFlip a une prpriété étonnante, il commute avec tout le monde ! c-à-d ΦV = VΦ quelle que soit la formule V.
2. Le 4Spot Ω : face(A)<->face(P) et face(G)<->face(D)
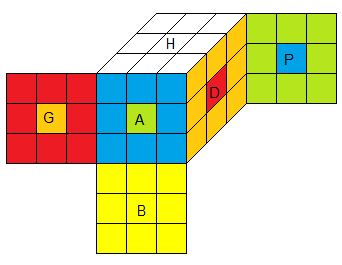
Ω = BP²A²BH'G²D²H' = [ha][hd] tH² (12*)
|Ω|=12
3. Le SuperFlip4Spot ∏
∏ = A DG'PBA D'HBPD' B'D'PH² B²P²D GB²DG (26*)
Michael Reid démontre que c'est une formule minimale |∏|=26 (c'est donc un SuperLoin, antipode)
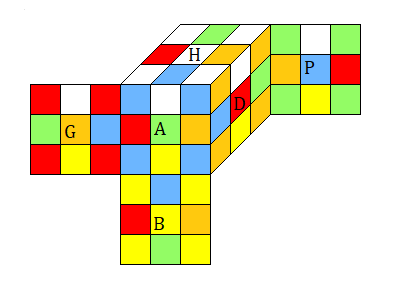
On ne connait pas d'autres SuperLoin (antipode) !! c'est le seul on connait !!!
|∏|=26
∏ = Φ Ω = Ω Φ , (ils se commutent)
4. MiniFlip (4 arêtes-Haut flippées) , cet état représente le nombre -1
N = A' H' G' H P' H² P G H A H' D H² D' ;(e • N = -1)
5. Nombre complexe i (i²=-1)
C = D P' A D' P A' H P H P' A D' A' D' ; (e • C = i)
REMARQUE: Il semble évident que l'état résolu représente 1, mais on peut le justifier ici par:
C4 = (D P' A D' P A' H P H P' A D' A' D')4 ; (e • C4 = 1)
6. On peut remplacer une rotation de base par les 5 autres, par ex:
B = (DG'A²P²DG')H(DG'A²P²DG') (Roger Penrose)
Cela signifie qu'on a besoin que 5 rotations pour s'en sortir !!
7. On sait que M est engendré pas 6 rotations de base M = < H,B,A,P,G,D > mais on démontre que M est aussi engendré pas deux formules (2 générateurs) K, S
M = < K,S > où K = HPGHG'H'P' et S = D²AGB'D' (Frank Barnes)
8. Un dragon de M
DRAGON = SK'
9. L'ordre maximal 1260
Quand on a H4 = I on dit que H est l'ordre 4, [DH]6 = I le crochet [DH] est l'ordre 6.
On démontre que l'ordre maximal d'ume formule est 1260, voici une formule qui donne l'ordre maximal 1260 :
Z = DH²B'PB' => (DH²B'PB')1260 = I
Il est remarquable que l'ordre maximal d'une formule est un quatrix !! (un nombre entier qui s'écrit avec quatre chiffres '4' et avec les 8 oppérations suivantes
{+, -, x, /, √ , ab, !, [ ] } , [x]=partie entière de x