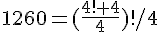Les formules célèbres
Publié : Jeu 5/05/2016 12:03
Aujourd'hui on va voir un certain nombre de formules célèbres.
Pour chaque formule on peut associer une longueur, la façon la plus naturelle c'est compter le nombre de rotations que compose
la formule, par exemple
V = HAB²P'G² , longueur(V)=7 on note aussi |V|=7 on dit qu'on a utilisé la métrique quart, 7 q-rotations
Il y a aussi une autre manière de compter les rotations , on compte A² pour 1 c'est-à-dire |A²|=1 donc dans ce cas
|V|= 5f on dit qu'on a utilisé la métrique "face" , 5 f-rotations. Bref ce n'est pas important les vocabulaires "métrique-quart", "métrique-face"
Pour nous on va prendre la métrique quart, la plus naturelle |V|=7 (q-rotations)
Remarque: il se peut qu'on a deux formules identiques mais qui ont de longueur différente !! par ex: A3 = A' et
|A3|=3 et |A'|=1
Une question naturelle est: une formule donnée, trouver une formule une plus courte, minimale ? (*=minimale)
Formules célèbres
1. Le SuperFlip Φ : toutes les arêtes sont renversées.
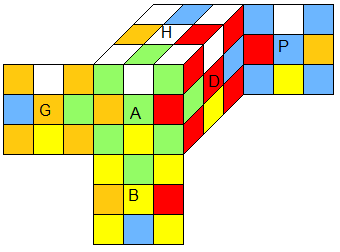
Φ = D'H²PG' AH'PBA HB'GB² A'DP'BA' H'P'HB' (trouvé par Michael Reid par ordinateur), en 1995 Jerry Bryan démontre que c'est une formule minimale
|Φ|=24
Le SupeFlip a une prpriété étonnante, il commute avec tout le monde ! c-à-d ΦV = VΦ quelle que soit la formule V.
2. Le 4Spot Ω : face(A)<->face(P) et face(G)<->face(D)
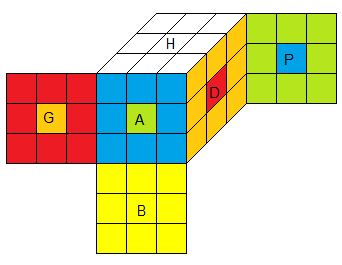
Ω = BP²A²BH'G²D²H' = [ha][hd] tH² (12*)
|Ω|=12
3. Le SuperFlip4Spot ∏
∏ = A DG'PBA D'HBPD' B'D'PH² B²P²D GB²DG (26*)
Michael Reid démontre que c'est une formule minimale |∏|=26 (c'est donc un SuperLoin, antipode)
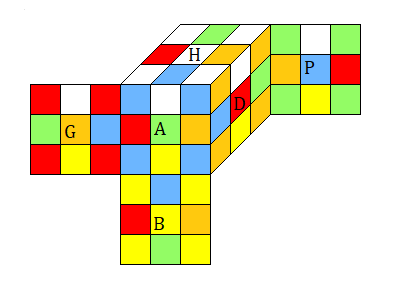
On ne connait pas d'autres SuperLoin (antipode) !! c'est le seul on connait !!!
|∏|=26
∏ = Φ Ω = Ω Φ , (ils se commutent)
4. MiniFlip (4 arêtes-Haut flippées) , cet état représente le nombre -1
N = A' H' G' H P' H² P G H A H' D H² D' ;(e • N = -1)
5. Nombre complexe i (i²=-1)
C = D P' A D' P A' H P H P' A D' A' D' ; (e • C = i)
REMARQUE: Il semble évident que l'état résolu représente 1, mais on peut le justifier ici par:
C4 = (D P' A D' P A' H P H P' A D' A' D')4 ; (e • C4 = 1)
6. On peut remplacer une rotation de base par les 5 autres, par ex:
B = (DG'A²P²DG')H(DG'A²P²DG') (Roger Penrose)
Cela signifie qu'on a besoin que 5 rotations pour s'en sortir !!
7. On sait que M est engendré pas 6 rotations de base M = < H,B,A,P,G,D > mais on démontre que M est aussi engendré pas deux formules (2 générateurs) K, S
M = < K,S > où K = HPGHG'H'P' et S = D²AGB'D' (Frank Barnes)
8. Un dragon de M
DRAGON = SK'
9. L'ordre maximal 1260
Quand on a H4 = I on dit que H est l'ordre 4, [DH]6 = I le crochet [DH] est l'ordre 6.
On démontre que l'ordre maximal d'ume formule est 1260, voici une formule qui donne l'ordre maximal 1260 :
Z = DH²B'PB' => (DH²B'PB')1260 = I
Il est remarquable que l'ordre maximal d'une formule est un quatrix !! (un nombre entier qui s'écrit avec quatre chiffres '4' et avec les 8 oppérations suivantes
{+, -, x, /, √ , ab, !, [ ] } , [x]=partie entière de x
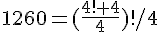
Pour chaque formule on peut associer une longueur, la façon la plus naturelle c'est compter le nombre de rotations que compose
la formule, par exemple
V = HAB²P'G² , longueur(V)=7 on note aussi |V|=7 on dit qu'on a utilisé la métrique quart, 7 q-rotations
Il y a aussi une autre manière de compter les rotations , on compte A² pour 1 c'est-à-dire |A²|=1 donc dans ce cas
|V|= 5f on dit qu'on a utilisé la métrique "face" , 5 f-rotations. Bref ce n'est pas important les vocabulaires "métrique-quart", "métrique-face"
Pour nous on va prendre la métrique quart, la plus naturelle |V|=7 (q-rotations)
Remarque: il se peut qu'on a deux formules identiques mais qui ont de longueur différente !! par ex: A3 = A' et
|A3|=3 et |A'|=1
Une question naturelle est: une formule donnée, trouver une formule une plus courte, minimale ? (*=minimale)
Formules célèbres
1. Le SuperFlip Φ : toutes les arêtes sont renversées.

Φ = D'H²PG' AH'PBA HB'GB² A'DP'BA' H'P'HB' (trouvé par Michael Reid par ordinateur), en 1995 Jerry Bryan démontre que c'est une formule minimale
|Φ|=24
Le SupeFlip a une prpriété étonnante, il commute avec tout le monde ! c-à-d ΦV = VΦ quelle que soit la formule V.
2. Le 4Spot Ω : face(A)<->face(P) et face(G)<->face(D)

Ω = BP²A²BH'G²D²H' = [ha][hd] tH² (12*)
|Ω|=12
3. Le SuperFlip4Spot ∏
∏ = A DG'PBA D'HBPD' B'D'PH² B²P²D GB²DG (26*)
Michael Reid démontre que c'est une formule minimale |∏|=26 (c'est donc un SuperLoin, antipode)

On ne connait pas d'autres SuperLoin (antipode) !! c'est le seul on connait !!!
|∏|=26
∏ = Φ Ω = Ω Φ , (ils se commutent)
4. MiniFlip (4 arêtes-Haut flippées) , cet état représente le nombre -1
N = A' H' G' H P' H² P G H A H' D H² D' ;(e • N = -1)
5. Nombre complexe i (i²=-1)
C = D P' A D' P A' H P H P' A D' A' D' ; (e • C = i)
REMARQUE: Il semble évident que l'état résolu représente 1, mais on peut le justifier ici par:
C4 = (D P' A D' P A' H P H P' A D' A' D')4 ; (e • C4 = 1)
6. On peut remplacer une rotation de base par les 5 autres, par ex:
B = (DG'A²P²DG')H(DG'A²P²DG') (Roger Penrose)
Cela signifie qu'on a besoin que 5 rotations pour s'en sortir !!
7. On sait que M est engendré pas 6 rotations de base M = < H,B,A,P,G,D > mais on démontre que M est aussi engendré pas deux formules (2 générateurs) K, S
M = < K,S > où K = HPGHG'H'P' et S = D²AGB'D' (Frank Barnes)
8. Un dragon de M
DRAGON = SK'
9. L'ordre maximal 1260
Quand on a H4 = I on dit que H est l'ordre 4, [DH]6 = I le crochet [DH] est l'ordre 6.
On démontre que l'ordre maximal d'ume formule est 1260, voici une formule qui donne l'ordre maximal 1260 :
Z = DH²B'PB' => (DH²B'PB')1260 = I
Il est remarquable que l'ordre maximal d'une formule est un quatrix !! (un nombre entier qui s'écrit avec quatre chiffres '4' et avec les 8 oppérations suivantes
{+, -, x, /, √ , ab, !, [ ] } , [x]=partie entière de x