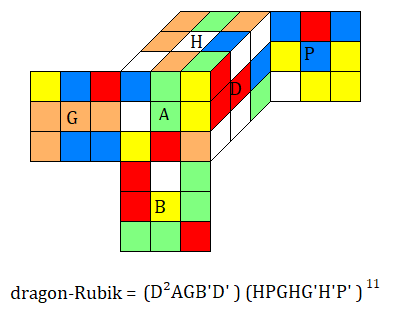
Un dragon du Rubik's Cube
Publié : Mer 19/06/2024 08:28
Soit W un sous groupe de formules à trois générateurs X,Y,Z : W = <X,Y,Z> ; ord(X) <= ord(Y)
On définit par récurrence la suite de formules :
1) F1 = Z X
On passe de Fn à Fn+1 ainsi :
2) Fn = Yp Z Xq
Fn+1 = Yp' Z Xq'
avec
p' = ((q+1) modulo ord(X)) modulo ord(Y)
q' = p modulo ord(X)
Si W = <X,Y> ; on prend Z=I, I=formule neutre
Comme il y a un nombre fini d'états on tombe forcement sur un état déjà donné par une formule Fk. Par ex on est à l' étape n ,la première fois qu'on tombe sur la formule F1 = ZX , l'état e•Fn-1 se nomme un état dragon de W,
par ex si à l'étape 17 on tombe (pour la 1er fois) sur F1 = ZX ,
alors un état dragon de W est :
dragon = e•F16
Frank BARNES a démontré que :
M = < H,B,A,P,G,D >
M = < K,S > où K = HPGHG'H'P' et S = D²AGB'D' (Frank BARNES)
Question: Trouver un dragon de M=<K,S> ==> (on peut faire un programme informatique pour le trouver)


On définit par récurrence la suite de formules :
1) F1 = Z X
On passe de Fn à Fn+1 ainsi :
2) Fn = Yp Z Xq
Fn+1 = Yp' Z Xq'
avec
p' = ((q+1) modulo ord(X)) modulo ord(Y)
q' = p modulo ord(X)
Si W = <X,Y> ; on prend Z=I, I=formule neutre
Comme il y a un nombre fini d'états on tombe forcement sur un état déjà donné par une formule Fk. Par ex on est à l' étape n ,la première fois qu'on tombe sur la formule F1 = ZX , l'état e•Fn-1 se nomme un état dragon de W,
par ex si à l'étape 17 on tombe (pour la 1er fois) sur F1 = ZX ,
alors un état dragon de W est :
dragon = e•F16
Frank BARNES a démontré que :
M = < H,B,A,P,G,D >
M = < K,S > où K = HPGHG'H'P' et S = D²AGB'D' (Frank BARNES)
Question: Trouver un dragon de M=<K,S> ==> (on peut faire un programme informatique pour le trouver)
On dit aussi c'est un dragon du Rubik's Cube.